Chapter 10

 

Analog Integrated Circuits

 

 

In earlier chapters of this text the low-frequency behavior of differential pairs, current mirrors, output buffers, and other circuit building blocks was investigated using Spice. These were also combined, in a rather simplistic way, to form an operational amplifier whose large and small-signal static behavior was analyzed using Spice.  This same approach is also used to realize other more sophisticated analog ICs.  The very-popular bipolar 741 op amp circuit used in several of the examples of Chapter 2 is one such example.  In this chapter we shall perform a detailed analysis of the 741 op amp using Spice.  This will include an investigation into both its static and dynamic circuit behavior. We will also take a brief look at the expected thermal noise behavior of this op amp using the noise analysis capabilities of Spice.  Following this, we shall investigate several CMOS and BiCMOS op amp designs that are finding important application in VLSI systems. Finally, we shall investigate the behavior of a D/A and an A/D converter circuits.

 

10.1 A Detailed Analysis Of The 741 Op Amp Circuit

 

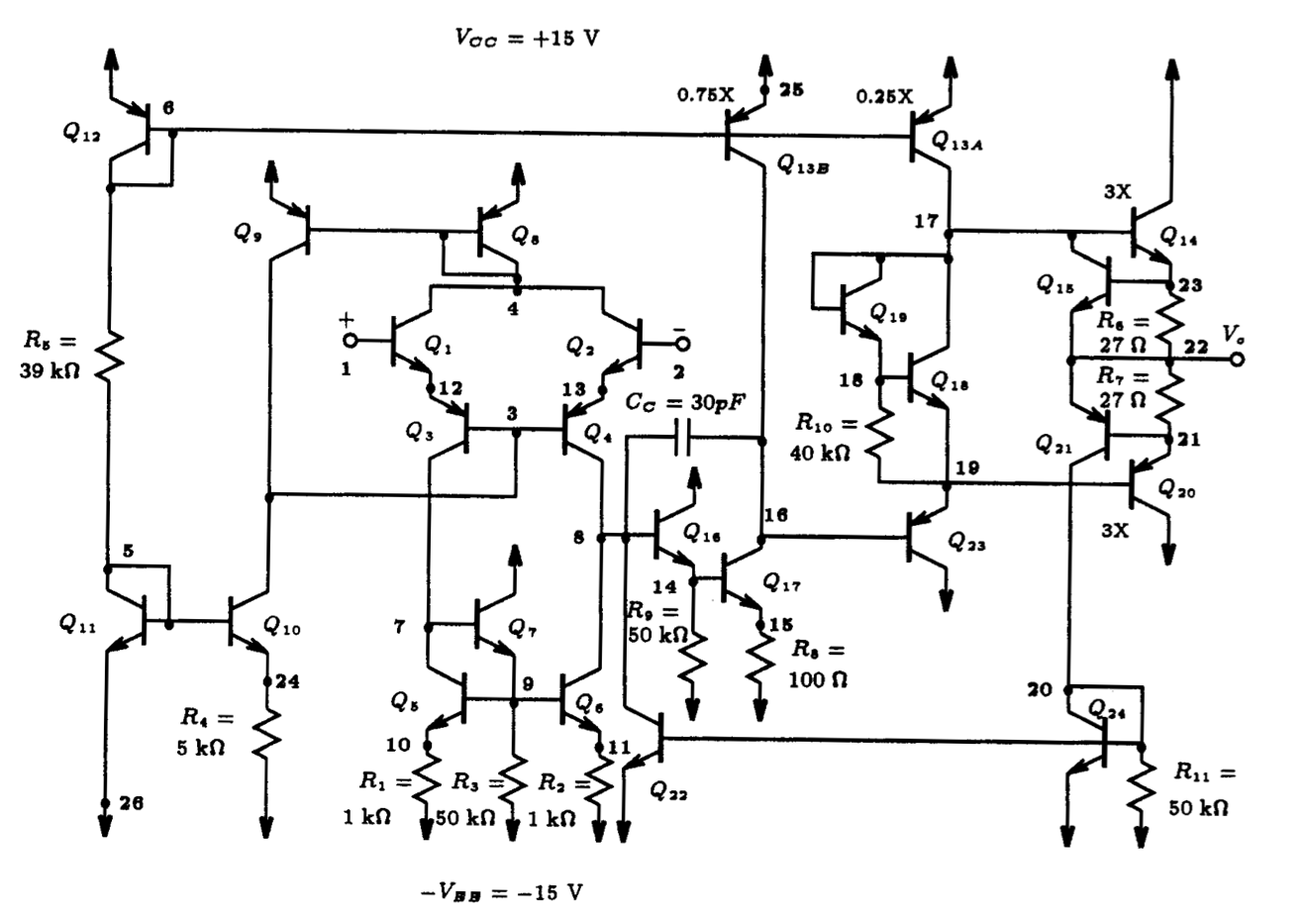
A detailed circuit schematic of the 741 op amp is shown in Fig. 10.1.  It consists of five main parts: (i) bias circuit, (ii) the input gain stage, (iii) the second gain stage, (iv) the output buffer, and (v) the short-circuit protection circuit. Each one of these stages, in one form or another, was briefly discussed and analyzed with Spice in previous chapters of this text.  For a detailed explanation of each section of the 741 op amp, see the discussion in Chapter 10 of Sedra and Smith, 3^rd Edition.

 

In the following we shall demonstrate how one can utilize Spice to analyze the behavior of a complex analog circuit, such as the 741 op amp circuit shown in Fig. 10.1. Many of the procedures and set-ups used here would have been seen by our readers in early examples of this text, so our emphasis here serves more as a review of these methods; albeit, in a more complex setting. One exception to this is the Spice method used to compute the thermal noise behavior of the 741 op amp.

 

Assuming the typical set of device parameters for both the npn and pnp transistors shown in Table 10.1, we shall proceed to compute the DC operating point of the amplifier, its gain and frequency response, slew-rate and noise behavior. A reduced version of these parameters were used by Sedra and Smith in their hand analysis of the 741 op amp circuit in Chapter 10 of their text. Direct comparisons can be made between the results obtained through hand analysis and those obtained with Spice.

 

The Spice input file describing the circuit of the 741 op amp is listed in Fig. 10.2. The differential input is driven by the familiar multiple-input voltage-source arrangement discussed in section 6.1 and shown again in Fig. 10.3. This multiple source arrangement provides maximum flexibility when it comes to performing different types of analysis (e.g., differential-mode and common-mode transfer characteristics) on a differential amplifier.

 

 

 

 

 

DC Analysis of the 741

 

The first analysis that we will request that Spice perform is a DC operating point analysis. This will provide us with some insight into the DC behavior of all the transistors in the op amp circuit for grounded inputs - in case it's needed. In addition to this, we shall also request a DC sweep of the input differential voltage. This will indicate the boundaries of the high-gain region of the amplifier so that other analysis can be performed on the amplifier while it's biased around a known operating point; preferably a point within the linear region of the amplifier.  Initially we set-up the DC sweep so that the input differential voltage is varied between the limits of the two power supplies. However, after the first submission to Spice, we refined the sweep range to vary between -400 uV and -200 uV in 10 uV increments so that we would obtain better resolution around the high-gain region of the amplifier[1]. During this analysis the input common-mode level is held at ground potential.

 

On completion of Spice, the large-signal differential-mode transfer characteristics of the 741 op amp, together with its DC operating point information, are calculated. The former is on display in Fig. 10.4. From this graph we observe several characteristics of the op amp. The first is that the linear region of the amplifier, as seen from the input terminals of the op amp, is bounded between -360 uV and -268 uV.  Conversely, this corresponds to a maximum output voltage swing bounded in the negative direction by -13.2 V, and +13.2 V in the positive direction. This suggests that the small-signal DC gain of this amplifier is approximately 13.2-(-13.2) / -268u -(-360u )=+287 kV/V.  We also notice that the transfer characteristics of this amplifier cross the 0 V output axis somewhere between -320 uV and -310 uV. A careful look using the Probe capability of PSpice indicates that the cross-over point occurs at -314.1 uV. Thus, this particular amplifier has an input-referred DC offset voltage of +314.1 uV.  This is the systematic offset of the op amp design and does not include offsets that result from component mismatches.

 

Reviewing the DC operating point information (which is not shown here) reveals that for grounded amplifier inputs, transistors Q_13A and Q_13B are saturated, causing transistors Q₁₄, Q₁₈-Q₂₀, and Q₂₃ to cutoff. Except for these and the transistors of the protection circuit, the remaining transistors are operating in their active regions. Other DC information, such as input bias currents, static power dissipation, etc., was calculated through the .OP command; however, these results are obtained when the op amp is biased outside of its normal operating region i.e., linear region.  Since the op amp is generally operated in its linear region, it is more appropriate to repeat the DC operating point command with the op amp is biased in its linear region. This is easily accomplished by applying a differential input offset voltage of -314.1 uV across the two inputs to the op amp. We can then repeat the DC analysis with the following element statement replacing the one listed in Fig. 10.2:

 

Vd 101 0 DC -314.1uV.

 

On completion of Spice, we obtain the following small-signal bias solution:

 

 

From the above, we see that the 741 op amp dissipates a static power of 55.2 mW.  We can also calculate the input bias and offset currents of the op amp from the currents passing through the two VCVS, EV+ and EV-.  The input bias current I_B is (-34.40n) + (-34.56n) / 2 =34.48 nA and the offset current I_OS is |(-34.40n) - (-34.56n)| = 0.16 nA. This particular offset current is due solely to the systematic offset of the op amp design itself, as opposed to any random offset effect that can occur during manufacture.

 

Also included in the Spice output file is a detailed listing of the operating point of each transistor. Rather than list all of this information here, instead, in Table 10.2 we list the collector current (in uA) of each transistor found in the 741 op amp circuit. These are also compared with the current levels computed using hand analysis by Sedra and Smith. As is self-evident, there is reasonable agreement between the two sets of results.

 

To determine the input common-mode range (CMR) of the 741 op amp, we shall sweep the input common-mode level V_CM between the two power supply limits. To ensure that the op amp is biased in the linear region, we maintain the input differential offset voltage at -314.1 uV.  To accomplish our task of varying the input common-mode level, we simply alter the .DC sweep command listed in the Spice deck of Fig. 10.2 according to:

 

.DC Vcm -15V +15V 0.1V.

 

No other alterations are necessary.

 

 

 

 

 

 

 

 

Re-submitting the revised input file to Spice results in the large-signal common-mode DC transfer characteristic displayed in Fig. 10.5. Here we see that linear operation is maintained over an input common-mode range (CMR) between -10.0 V and +8.05 V corresponding to an output voltage swing varying between -13.26 V and 14.27 V.  The lower limit of the CMR is caused by Q_13A of the second stage saturating.  Similarly, the upper limit of the CMR is caused by transistor Q₁₇ also of the second stage saturating.  We can also estimate the common-mode voltage gain in the linear region of the op amp to be (-13.26)- 14.27 / 8.05-(-10.0) =-1.53 V/V.

 

We should note that these results are quite different from those normally encountered in an actual 741 op amp. Typically, the input CMR is determined by the transistors of the front-end stage leaving their linear regions rather than transistors of the second stage - as we have seen above.  We attribute this difference to the fact that the 741 op amp consists of 6 different types of transistors (i.e., small npn, large npn, lateral pnp, substrate pnp, dual-emitter pnp and a dual-collector pnp) each having different terminal characteristics. On the other hand, the above Spice simulation of the 741 op amp models the diversity of the different transistors with only two model types. Thus, some behavior of the actual 741 op amp is not properly captured in our simulations.

 

 

 

 

 

The above results are all examples of a large-signal analysis.  Much of the analysis performed by Sedra and Smith is based on small-signal analysis. To obtain the small-signal parameters of the op amp we make use of the .TF command of Spice. For instance, the small-signal differential voltage gain and small-signal output resistance of the op amp can be computed by adding the following command to the Spice deck shown listed in Fig. 10.2:

 

.TF V(22) Vd

 

It is important to maintain the input differential offset voltage at -314.1 uV in order to keep the amplifier in its linear region. The input common-mode level is also held at ground potential.  The results of Spice are listed below:

 

Here we see that the small-signal differential voltage gain of +294.6 kV/V is quite close to the value +287 kV/V estimated from the slope of the op amp large-signal transfer characteristics shown in Fig. 10.4. The input resistance stated here is not the input differential resistance of the op amp. Rather, this is the 1 W resistance connected directly to V_d.  To obtain an estimate of the input resistance of the op amp, we shall instead use the results of the AC analysis presented below.  The output resistance of the op amp is seen to be quite low at 106.4 W.

 

We can repeat the above .TF analysis with respect to the input common-mode level around the operating point defined by V_CM=0 V and V_d=-314.1 uV.  One simply utilizes the command:

 

.TF V(22) Vcm

 

The results of the analysis are then found in the Spice output file as follows:

The common-mode voltage gain is -1.555 V/V, the input common-mode resistance is seen to be a very large 606.4 MW, and the output resistance is, as expected, the same as the previous calculation of 106.4 W.

 

Dividing the differential voltage gain of 2.946 x 10⁵ V/V by the magnitude of common-mode voltage gain of 1.555 V/V we obtain the common-mode rejection ratio (CMRR) for the 741 op amp to be 105.6 dB.

 

We can carry the small-signal analysis over to the frequency domain and have Spice compute the differential magnitude and phase response of the op amp. Several alterations must be made to  the Spice input file shown listed in Fig. 10.2. For starters, the input differential excitation should be changed to include an AC voltage component. A one-volt AC signal will be applied.  The amplitude of this AC input is not important because an AC analysis is performed using a linearized model of the transistor circuit. A 1-volt amplitude is commonly chosen for the input signal because, in this way, the output voltage directly represents the transfer function of the circuit.  We maintain the input DC offset voltage at -314.1 uV in order to maintain the op amp in its linear region. Thus, the input excitation statement should be changed to read as follows:

 

Vd 101 0 DC -314.1uV AC 1V.

 

Gain and Frequency Response of the 741

 

Following this, we shall request that Spice compute the frequency response of the amplifier over a frequency interval beginning at 0.1 Hz and ending at 100 MHz using the following statement:

 

.AC DEC 10 0.1Hz 100MegHz

 

A plot statement can be included in the input file to graphically display the output voltage results of the frequency response analysis. Its syntax would appear as follows:

 

.PLOT AC VdB(22) Vp(22).

 

 

We shall also include a .PRINT statement for the magnitude of the small-signal current flowing through the two VCVSs in series with the op amp input terminals. This will allow us to calculate the input differential resistance of the op amp knowing that the small-signal input differential voltage applied to the amplifier is 1 V.  The command line for this is

 

.PRINT AC Im(EV+) Im(EV-).

 

 

The revised Spice input file for calculating the small-signal frequency response of the 741 op amp is listed in Fig. 10.6.

 

The results of the frequency-domain analysis are shown in Fig. 10.7. The low-frequency behavior is dominated by a single-pole response having a low-frequency gain of 109.4 dB and a 3-dB bandwidth of approximately 2.6 Hz. The unity-gain frequency f_t is read directly off the graph using Probe to be 0.652 MHz. We also find that this amplifier has a phase margin of 66.7°.  The presence of a second pole is also evident. It is located at approximately 1.82 MHz.

 

The low frequency current drawn by the op amp input terminals was found by Spice to be as follows:

 

We see here that there is a small difference between the two currents drawn by the op amp input terminals. This difference is due to op amp systematic offset.  To determine the input differential resistance to the amplifier under such asymmetric conditions, we shall work with the average of the two base currents. In this way, we can eliminate the presence of the offset current in the resistance calculation.  Thus, we compute the average input base current to be 274.9 nA and therefore obtain the input differential resistance at 3.64 MW.

 

 

 

 

Slew-Rate Limiting of the 741

 

An important attribute of op amp behavior that usually limits the high-frequency operation of op amp circuits is its slew-rate limiting. Connecting the op amp in a unity-gain configuration and applying a large voltage pulse to its input will reveal both the positive-going and negative-going slew-rate of this op amp, as demonstrated in Fig. 10.8.  The Spice input file depicting this arrangement is provided in Fig. 10.9. Here a zero-valued voltage source described by

 

Vshort 2 22 0

 

is used to form a direct connection between the op amp output and its negative input terminal. This avoids having to renumber the negative input terminal of the op amp in the Spice deck with the same number used to describe the op amp output.  Another voltage source is used to create the input pulse:

 

Vd 1 0 PWL ( 0,-5V 1ns,+5V 30000ns,+5V 30001ns,-5V 1s,-5V ).

 

Notice that this input pulse signal is described in a piece-wise linear fashion, beginning at a low level of -5 V and quickly rising to +5 V one ns after this, staying there for 30 us and then returning to the -5 V level one ns later. It remains at this low level of -5 V for the rest of the duration of the pulse.  A transient analysis is requested to compute the response of the op amp circuit arrangement over a 100 us interval using a 0.1 ns sampling interval. 

 

Submitting this input file to Spice results in the plot shown in Fig. 10.10. Both the input pulse to the amplifier and its output response are shown. Here we see that the positive-going portion of the output signal has a very different shape than the negative-going portion. Instead of a gradual rise in the positive-going signal, initially there is small jump in the output voltage of 2.2 volts, followed by the output being held constant at -2.8 V for 3.6 us, then rising linearly to +5 V in 18.2 us.  Thus, the positive-going slew-rate is estimated at +0.55 V/us.

 

The negative-going response behaves more along the lines of what one expects, a steady decline from +5 V to -5 V. As a result, the negative-going slew-rate is found to be -0.39 V/us.

 

 

 

 

Noise Analysis of the 741 Op Amp

 

As our final analysis, we shall utilize the noise analysis capability of Spice to estimate both the output-referred and input-referred thermal noise power spectral density S_h(jw) of the 741 op amp circuit shown in Fig. 10.1. Analyzing the noise behavior of op amp circuits is a rather advanced topic and is not covered in the text by Sedra and Smith.  It is included here because of its importance and to demonstrate yet another analysis capability of Spice.

 

Resistors and semiconductor devices generate various types of noise. Thermal noise is one important example of this noise, and the minimization of this noise component is an important consideration in the design of op amp circuits. The cause of thermal noise is the random movement of charge carriers in resistors or semiconductor devices. This movement, in turn, causes instantaneous voltage excursions to appear across the terminals of the device whose value, on average, is zero. In a circuit, these voltage variations also have an effect on the node voltages of the circuit.  The total effect on any one particular node is simply the root-mean of the sum of the squares of each individual effect. The Noise Analysis capability of Spice performs exactly this computation in exactly this manner.  In general, these noise fluctuations are functions of frequency and therefore are computed in conjunction with the .AC analysis of Spice. As a result, the noise level is reported in the output file in units of either V/ÖHz or A/ÖHz depending on its context.

 

The syntax of the Noise Analysis command is given in Table 10.3. The keyword .NOISE specifies that a noise analysis is to be performed on a given circuit over the frequency interval specified on the .AC command line.  The next field output_voltage denotes a node voltage. The node(s) that this voltage appears across indicates the output port of the circuit.  Spice will compute the effective noise voltage spectral density that appears at this port due to internal noise sources.  Spice will not compute the effective output noise current spectral density associated with a short-circuit output.  The subsequent field, indicated by source_name, specifies the name of an independent voltage or current source. The output noise voltage spectral density will be referred back to the port defined by this independent source as either an input-referred noise voltage or current spectral density depending on the input source type.  

 

To access the noise information computed by Spice, one uses either a .PRINT or .PLOT command with reference to the information stored in the Spice variable ONOISE (output noise) or  INOISE (equivalent input-referred noise).

 

Returning to the Spice input deck that we used to compute the frequency response of the op amp circuit, shown listed in Fig. 10.6, consider adding the following .NOISE command statement to the file, together with the statement specifying the output plot request:

 

 

Re-submitting the input file to Spice results in the output-referred and input-referred noise voltage spectral densities for the 741 op amp shown in Fig. 10.11. As a point of reference, we see that the output-referred noise voltage density at 1 kHz is 14.7 uV/ÖHz. Conversely, the output noise power spectral density can be referred to the input of the op amp at this same frequency to find 19.0 nV/ÖHz.

 

 

 

 

A Summary of the 741 Op Amp Characteristics

 

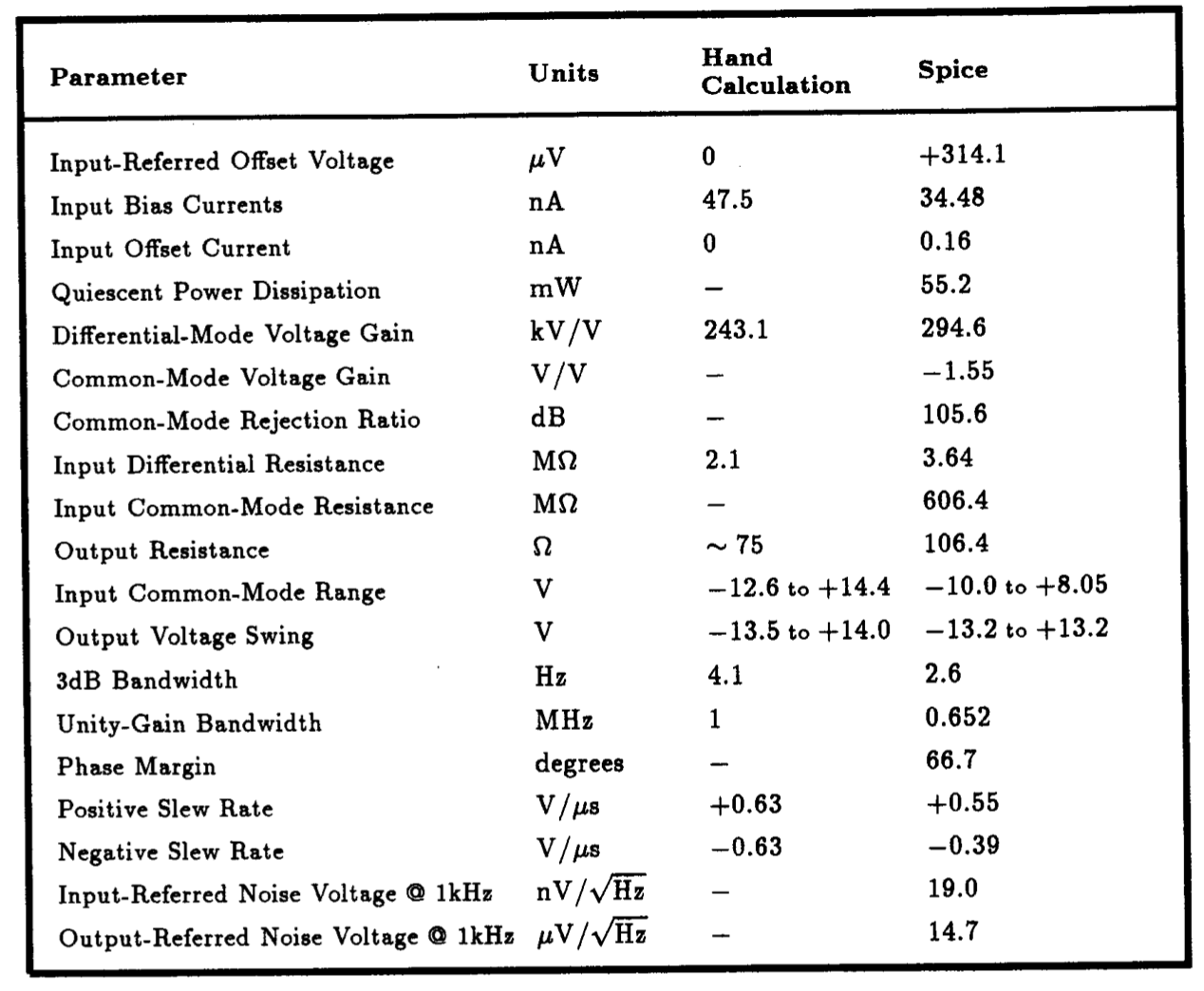
We summarize the results that we have obtained through the application of Spice to the 741 op amp in Table 10.4. Some of these results are also compared to those computed by hand in Sections 10.1-10.6 of Sedra and Smith. For the most part, the results obtained through hand analysis agree quite well with those computed with Spice. This is especially true for the parameters obtained through the small-signal analysis. The same cannot be said for many of the op amp's large-signal DC characteristics. We attribute this to the fact that the large-signal DC analysis performed by Sedra and Smith neglected the effect of transistor Early voltage, unlike that performed during the small-signal analysis.  Of course, one could improve the accuracy of the hand analysis by including the effect of transistor Early voltage in the large-signal calculations; however, the additional complexity is probably not commensurate with the additional accuracy gained, especially when one could go directly to Spice.

 

 

 

10.2 A CMOS Op Amp

 

In Fig. 10.12 we show a two-stage CMOS op amp circuit with the device geometries seen listed in Table 10.5.  The input differential stage of this amplifier was previously analyzed in Section 6.4 of this text for its large-signal differential-mode and common-mode transfer characteristics, among other things. Here an additional gain stage has been added in order to increase the gain of the amplifier, and a compensation network is included to maintain stability when the op amp is connected in a negative feedback loop. In Example 10.2 of Sedra and Smith this amplifier stage was analyzed by hand with rather simple transistor models where it was found to have a DC differential gain of +3125 V/V, an input common-mode range varying between -4.5 V to +3.0 V, and an output voltage swing ranging between -4.5 V and +4.4 V.

 

In the following we shall recalculate the above parameters of the CMOS amplifier with Spice using more realistic transistor models. In particular, we shall consider that each MOSFET is modeled after the transistors found in the 5-micron CMOS process at Bell Northern Research (BNR).  We shall then compare these results with those predicted by the simple formulae presented in Sedra and Smith in Example 10.2 of their text using the DC operating point information provided by Spice.

 

The Spice description of the CMOS amplifier is shown in Fig. 10.13. The differential input is driven by the multiple source arrangement shown in Fig. 10.3. A level 2 MOSFET model of each transistor type is provided with a lengthy list of device parameters. These were obtained through extensive measurements on transistors fabricated through the 5 um CMOS process at BNR. The first analysis requested is a DC sweep of the input differential voltage V_d between the two supply limits with the input common-mode level V_CM set to 0 V.

 

 

 

 

 

 

 

The results of this DC sweep are shown plotted in Fig. 10.14. We see here that the linear region of the amplifier extends between the input voltage levels of -1.24 mV and +1.71 mV. Correspondingly, this gives rise to a maximum output voltage swing ranging between -4.40 V and +4.54 V. Thus, the small-signal differential gain can be estimated to be in the neighborhood of +3.031 kV/V.  Also, we see that the input-referred offset voltage is approximately -220.0 uV.

 

Following this, we have performed a DC sweep of the input common-mode level with the differential input to the amplifier offset by +220.0 uV.  To accomplish this, we replaced the DC sweep command given in Fig. 10.13 by the following one:

 

.DC Vcm -5V +5V 0.1V.

 

and modified the input differential voltage statement V_d according to:

 

 

Vd 101 0 DC +220.0uV.

 

 

The results of this analysis are displayed in Fig. 10.15.  As is evident, the input common-mode range extends from the lower limit of the power supply V_SS to +3.1 V. We can further add commands .TF and .OP into the Spice deck and obtain the small-signal DC gain of the circuit and any relevant DC operating point information. These two new commands would appear in the Spice deck as follows:

 

One would then find in the output file the following information:

 

 

         

Here we see that the small-signal DC gain of +3.603 kV/V has the same order of magnitude as our earlier estimate. We can check this value against the gain predicted by the formulae derived in Sedra and Smith; A₀=g_m1(r_o2||r_o4) x g_m6(r_o6||r_o7).  Substituting the appropriate values from the above Spice generated small-signal data we see that A₀=+3.630 kV/V, which agrees quite closely with the value predicted by the .TF command of Spice.

 

We can also make use of the above DC and small-signal information to estimate the input CMR of this amplifier and its output voltage swing.  The lower limit of the input CMR is determined by M₁ leaving the saturation region.  This occurs when the voltage at the gate of M₁ drops below the voltage at its drain (V(7)=-3.5404 V) by a single threshold level. From the above Spice generated data, we see that the threshold voltage of M₁ is -1.51 V.  We can then compute the lower limit of the input CMR to be -5.1 V.  This limit seems to extend beyond V_SS of -5 V, unlike that calculated by hand where it was found that the lower CMR limit is -4.5 V. The reason for the difference is that in the hand calculation a threshold voltage of -1 V for M₁ was assumed neglecting its dependence on the source-substrate back-bias voltage (the body effect).  If the hand calculation used the actual threshold voltage of M₁ at -1.51 V, we would obtain the exact same lower limit to the CMR found through Spice. 

 

The upper limit of the input CMR is determined by M₅ leaving the saturation region. This occurs when the drain of M₅ rises one threshold voltage above its gate voltage of +3.4242 V. The threshold voltage of M₅ is -0.959 V. Hence, M₁ leaves saturation when its drain voltage exceeds +4.38 V. To relate this voltage to the input of the amplifier, we simply subtract off the gate-source voltage of either M₁ or M₂. The result is the upper CMR limit of (4.38 V - 1.88 V) or +2.5 V.  This is somewhat lower than that predicted by hand analysis at +3 V. It is also lower than that seen from the plot of the output voltage of the amplifier as a function of the input common-mode voltage shown in Fig. 10.15. There are two reasons for the discrepancy. The first is again due to the fact that the transistor body effect has been neglected.  In addition, the current flowing through both M₁ and M₂ is somewhat reduced because of the dependence of the drain current of M₅ on its drain voltage. This, in turn, decreases the gate-source voltage of M₁ and M₂. Thus, a larger input common-mode voltage can appear at the input terminals of the amplifier before any internal saturation occurs.

 

Following similar reasoning, the maximum range of the output voltage is one threshold voltage above the gate voltage of M₇. Thus, it is simply (3.42 V + 0.954 V) or +4.37 V. Likewise, the minimum output voltage is one threshold voltage below the gate voltage of M₆ and is therefore -4.49 V. These results seem to be reasonably close to the results that are visible from Fig. 10.14 using Probe (i.e., -4.40 V and +4.54 V) and those computed by hand (i.e., -4.5 V and +4.4 V).

 

 

10.3 Two Different Technology Versions of A Folded-Cascode Op Amp

 

In Fig. 10.16 we display two different versions of a folded-cascode op amp circuit; one realized using CMOS technology and the other using a combination of CMOS and Bipolar technology called BiCMOS. The dimensions of the various MOSFETs of the two circuits are provided in Table 10.16; the bipolar transistors are assumed all equal in size, except Q₆ and Q₇ which are three times the size of the other bipolar transistors.

 

In the following we shall compare the frequency response behavior of these two op amp circuits assuming that the MOSFETs are modeled with the complex BNR 5-micron CMOS models used in the previous section and the bipolar transistors are modeled using the complex set of parameters listed in Table 10.1.  But before we begin this, we shall first compute the frequency response behavior of the two amplifiers by hand in order to obtain some sense of expected amplifier behavior. We shall assume that a simplified representation of the NMOS transistors are characterized by: V_t=1 V, u_nC_OX=20 uA/V² and =0.04 V^-1; similarly, for the PMOS transistors:  $V_t=-1 V, u_pC_OX = 10 uA/V² and l=0.04 V^-1. A simplified model of the npn transistors of the BiCMOS circuit consists of I_S=10 fA, b=200$ and V_A=125 V.

 

According to the small-signal analysis performed by Sedra and Smith in Section 10.8 for a folded-cascode op amp, the voltage gain of either circuit is given by

(10.1)

 

where R_o is the output resistance of the op amp, given by

(10.2)

 

Moreover, the dominant pole of the amplifier is located at frequency

(10.3)

 

and the corresponding unity-gain frequency is

(10.4)

 

Performing a DC hand analysis on the folded-cascoded CMOS amplifier shown in Fig. 10.16(a) with the above mentioned MOSFET device and geometry parameters, we obtain their corresponding drain currents listed in Table 10.7.  To simplify the analysis, we have neglected the effect of channel-length modulation.  This analysis is rather straightforward owing to the fact that the reference current I_ref is simply mirrored into the other branches of the op amp.

 

Repeating the same DC analysis for the BiCMOS amplifier shown in Fig. 10.16(b) while neglecting the base currents of the bipolar transistors, one obtains exactly the same drain currents for each MOSFET as was found in the CMOS amplifier. The collector current of each npn transistor is equal to the drain current of the MOSFET that it replaces. Even though a MOSFET is replaced by a bipolar transistor, the same mirroring action is used in each circuit (i.e., the same current gains).

 

Knowing the device operating currents, we can compute the small-signal parameters of the devices of interest, and thus, calculate expected frequency response behavior of the op amp. Below we list the transconductance and output resistance of the appropriate transistors of the CMOS and BiCMOS op amps.  These can then be used to compute small-signal parameters $A_0$, R_o, f_D and f_t, as mentioned above.

 

 

Substituting the above small-signal parameters into Eqns. (10.1) - (10.4), we obtain the following small-signal frequency response data for the two op amps:

 

As is evident from this table of values, the BiCMOS op amp has a larger low frequency gain but a lower bandwidth than the corresponding CMOS version. Interestingly enough, both op amps have identical unity-gain bandwidths.

 

To investigate realistic op amp frequency response behavior, we make use of the two Spice decks listed in Figs. 10.17 and 10.18 where the transistors are modeled as mentioned earlier.  A DC sweep command of the input differential voltage is performed first in order to locate the high-gain linear region of the amplifier.  The common-mode input voltage level will be set at 0 V during this voltage sweep.

 

 

 

 

 

 

 

 

 

On completion of Spice, the large-signal differential characteristics of the CMOS and BiCMOS amplifiers are shown plotted in Fig. 10.19. As is evident, they have similar DC gains (i.e., slope of the linear region), with the BiCMOS circuit having a slightly larger gain. From these results we have determined with the aid of Probe that the DC offset of the CMOS and BiCMOS amplifiers are -857.1 uV and -500 uV, respectively.  Also apparent, the output voltage swing of the BiCMOS amplifier is about one volt larger than its CMOS counterpart. 

 

Offsetting the input to the two amplifiers with the appropriate DC voltage so that each amplifier is biased inside its linear region, we can compute the frequency response of each amplifier. This is accomplished by altering the input signal source statement in the Spice deck for the CMOS amplifier according to

 

Vd 101 0 DC -857.1uV AC 1V

 

and, likewise, for the BiCMOS amplifier with

 

Vd 101 0 DC -500.0uV AC 1V,

 

and adding the following AC analysis command in each input file

 

.AC DEC 10 1Hz 100MegHz,

 

we can then submit the revised Spice decks for analysis. The magnitude and phase behavior of the two amplifiers, as computed by Spice, are shown together in Fig. 10.20. Using Probe we were able to extract the following frequency response information from these results:

 

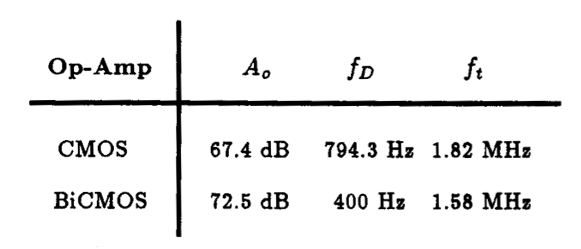
Examining the above results, we see that the BiCMOS amplifier has a slightly larger low-frequency gain but a lower 3 dB bandwidth than the corresponding CMOS amplifier. This manifest itself into the CMOS amplifier having a larger unity-gain bandwidth product than the BiCMOS amplifier.  In comparison with the results computed previously by hand, we find that the predicted DC gain and 3 dB bandwidth for the two amplifiers are quite different.  The reason for the discrepancy can be traced back to the rather crude estimates of the small-signal model parameters used to compute them. There are two reasons for this:  the simplified model parameters for the MOSFETs used in the hand calculations are not truly representative of actual transistor behavior, and secondly, the effect of transistor Early voltage and body-effect were neglected when the transistor bias levels were being computed.  Using the small-signal parameters generated by Spice through the .OP command, hand analysis using Eqns. (10.1)-(10.4) will generate results similar to those computed by Spice. We leave this for the reader to confirm using Spice.

 

The final point that we want to discuss here is the location of the second or nondominant pole of each amplifier. According to the frequency response results shown in Fig. 10.20 the CMOS amplifier has a nondominant pole at 36 MHz. Whereas, the BiCMOS amplifier has its nondominant pole located at a much lower frequency of only 4.5 MHz.  This result is rather contrary to what one would expect when a MOSFET is replaced by a corresponding bipolar transistor biased at the same current level. Since, after all, a bipolar transistor has a higher transconductance than a corresponding MOSFET when biased at the same current level. However, this is not the entire story because the location of the nondominant pole is also determined by the parasitic capacitance associated with the transistor.  As it turns out, in this particular case, the bipolar transistors used to replace the NMOS transistors have associated with it a much larger parasitic capacitance (this can be confirmed by viewing the small-signal model data generated by Spice for each transistor).  Thus, what signal strength is gained from the increased transconductance is lost in the frequency domain to the added parasitic capacitance of the bipolar transistor.  This is not necessarily what would happen in an actual design as the models for the MOSFETs and npn transistors used in this example were simply contrived and do not represent an actual BiCMOS technology.

 

10.4 Data Converters

 

Analog-to-digital (A/D) and digital-to-analog (D/A) converter circuits are important components of electronic systems. In the following we shall simulate the ideal behavior of a D/A and an A/D converter using Spice.  More specifically, we shall simulate the operation of the conversion of a 4-bit digital word into a corresponding analog signal using a 4-bit R-2R ladder D/A converter circuit. Secondly, we shall also observe the conversion of an analog signal into a 3-bit digital signal using a flash converter. Our objective here is to investigate basic circuit operation as opposed to observing nonideal behavior.

 

R-2R Ladder D/A Converter

 

Figure 10.21 displays the circuit schematic of a 4-bit D/A converter utilizing an R-2R ladder network. The double throw switches are assumed ideal and are controlled by the appropriate voltage source whose level represents a single bit of a 4-bit digital number. It is precisely this digital number that is to be converted into an equivalent analog signal. The op amp is assumed pseudo-ideal and represented by the high-gain VCVS shown in Fig. 10.21(b). A Spice description of this circuit is shown listed in Fig. 10.22. Four digital signal generators are provided, generating the entire sequence of digital words possible with 4-bits over an 8 ms interval. A low logic level is represented by 0 V and a high logic level by +5 V.

 

Of special interest, and not seen by the reader until now, is the PSpice element statement used to represent a voltage-controlled switch. This element is not available in all versions of Spice, but greatly simplifies circuit modeling, and thus, is employed here to represent a single-pole single-throw switch[2]. The general syntax of the PSpice voltage-controlled switch statement is shown in Fig. 10.23. Two statements are necessary to describe a voltage-controlled switch to PSpice:  a statement beginning with the letter S (for switch) specifying the connections made to the rest of the network and the name of the model used to characterize the switch. Another statement, cross-referenced to this element statement, contains a list of four parameters that describe the terminal behavior of the switch.  These are:  Von, the control voltage level required to turn on the switch; Voff, the voltage level that turns off the switch; and Ron and Roff, the on- and off-resistance of the switch, respectively.

 

 

 

 

 

 

 

 

In the PSpice description of the D/A converter seen listed in Fig. 10.22, the double-throw switch is represented by two complementary switches driven by the same digital control signal. The switches are complementary in the sense of their state of conduction. That is, one switch is conducting while the other is blocking.

 

The results of the transient analysis are shown in Fig. 10.24. The top graph displays the sequence of digital signals applied as input to the D/A converter and the bottom graph displays the corresponding analog output signal. The glitches seen superimposed on the analog output signal are due to the very short interval when all the switches disconnect from the op amp negative input terminal on their way to their next position.

 

3-Bit A/D Flash Converter

 

In Fig. 10.25 we display a 3-bit A/D flash converter circuit. Seven comparators are required for 3-bit accuracy. A 10 kW resistor string is used to realize the reference voltages for the various comparators. An input voltage signal V_i is applied to the positive input terminal of each comparator, and if the input signal is larger than the reference voltage applied to the negative input terminal, the output of the comparator goes into its high logic state, otherwise it remains in its low state.

 

In the following we shall compute the output state of each comparator as a function of the input voltage level using Spice. We shall model the terminal characteristics of each comparator using the equivalent circuit shown in part (b) of Fig. 10.25. The front-end portion of the comparator is modeled as a high-gain amplifier with a VCVS. The output of the amplifier is maintained within the limits of the two power supplies by clamping the output voltage to one of the supply levels using the diode and DC voltage source limiter.  The diodes will be assumed ideal, and made nearly so, by setting n small in the diode model statement (i.e., n=0.01).

 

 

The Spice file describing this circuit is shown listed in Fig. 10.26.  Here we are requesting a DC sweep of the input voltage beginning at the lower power supply limit of -5 V and ending at the +5 V power supply level. In this way, we should be able to exercise all possible states of the A/D converter. 

 

On completion of Spice, we have plotted the output voltage of each comparator as a function of the input voltage level, as shown in Fig. 10.27. Clearly, for an input voltage level between -5 V and -3.75 V all comparator outputs are logically low. Subsequently, with the input increased to some level somewhere between -3.75 V and -2.5 V, comparator C₇ goes logically high with all other comparators remaining in the logic low state. Continuing, for the next input voltage interval between -2.5 V and -1.25 V, we see that comparator C₆ has now also gone into its high state.  As we further increase the input voltage level, C₅ will be the next one that goes into its high state. This will be followed by C₄, C₃, etc.., until all comparator outputs are logically high when the input level exceeds +3.75 V. Since the combined output of this A/D has 8 possible states, it can be represented by a 3-bit binary number. This conversion would be performed by a digital circuit that would follow the A/D converter.

 

 

 

 

10.5 Spice Tips

 

·               Inputs to differential amplifiers should consist of both a differential and a common-mode component. An interesting arrangement of several voltage sources was given in this chapter, illustrating how the differential and common-mode components can be independently adjusted.

 

·               Performing a proper small-signal analysis on a high-gain amplifier circuit requires that the linear region of the amplifier be first located before any transfer function or frequency analysis is performed.

 

·               The linear region of an op amp is located by first sweeping the input differential voltage v_d between the limits of the power supplies with the common-mode voltage V_CM equal to 0 V. This analysis is repeated with a reduced sweep range centered more closely around the high-gain linear region of the amplifier until a smooth transition through the high-gain linear region is achieved. Following this, one must check to see whether the input common-mode voltage of 0 V keeps the amplifier in its linear region.

 

·               To quickly converge on the location of the high-gain region of an op amp, one can connect the op amp in a unity-gain configuration with the positive terminal of the op amp connected to ground and compute the input-referred offset voltage of the op amp V_OS.  Knowing this voltage, we can infer that the differential transfer characteristics of the op amp will cross the horizontal voltage axis (V_o=0 V) at -V_OS. This is usually a valid point within the high-gain region of the op amp.

 

·               Once the linear region of the amplifier is located, the correct DC conditions can be applied to the inputs of the amplifier to establish the proper bias point about which the small-signal analysis of Spice can be performed.

 

·               The small-signal input resistance of an op amp is computed using Spice by applying a known AC voltage across the input terminals of the differential amplifier and computing the AC currents that flow into the amplifier terminals. In many practical amplifier situations, these currents will not be equal. So, instead, the average of these two currents is used in the input resistance calculation.

 

·               The output thermal noise behavior of electronic circuits can be estimated using the noise analysis capability of Spice.

 

·               A voltage-controlled switch can be modeled in PSpice using a special element and model statement for the switch. An equivalent realization of a voltage-controlled switch can be described to Spice using a nonlinear VCCS statement having the following form:  Gswitch n+ n- poly(2) nc+ nc- n+ n- 0 0 0 0 1/Ron.

 

10.6 Bibliography

 

P.R. Gray and R.G Meyer, Analysis and Design of Analog Integrated Circuits, 2nd ed. New York: Wiley, 1984.}

 

10.7 Problems

 

10.1.      Determine, with the aid of Spice, the differential-mode and common-mode voltage gain of the 741 op amp when the power supplies are reduced to ±5 V.

 

10.2.      Assume that the IC process used to fabricate the 741 op amp circuit undergoes some variation that causes the Early voltage of each device to decrease by 30%, but all other parameters remain invariant. Making the appropriate changes to the Spice parameters listed in Table 10.1, recalculate the large and small-signal parameters of the 741 op amp seen listed in Table 10.4 and compare them to those listed in this table.

 

10.3.      One way to eliminate the input-referred offset voltage of an op amp such as the 741 is to connect what is known as a nulling resistor between the emitters of Q₅ and Q₆ of the first stage of the op amp seen in Fig. 10.1. With the aid of Spice determine the value of this nulling resistor that will cause the input offset voltage to be reduced to a value less than 10 uV. Hint: Connect the op amp in a unity-gain configuration and adjust the value of the nulling resistor to eliminate the offset voltage.

 

10.4.      Through a processing imperfection, the b of Q₄ in Fig. 10.1 is reduced to 25 while the b of Q₃ remains at its regular value of 50. Find the input offset voltage that this mismatch introduces using Spice.

 

10.5.      For a 741 op amp employing ±7.5 V supplies, determine the maximum output voltage swing possible.

 

10.6.      Determine the phase and gain margin of the 741 op amp when the compensation capacitor C_C is reduced from 30 pF down to 20 pF.  Will the amplifier be stable when it is connected in a unity-gain configuration?  Use the device parameters provided in Table 10.1.

 

10.7.      This problem involves investigating the short-circuit protection capability of the 741 op amp. Consider connecting the op amp in a unity-gain configuration with the output terminal connected directly to ground.  With the input to the voltage follower connected to +5 V, compare the power dissipated by the output stage with and without the internal short-circuit protection circuitry in place. 

 

10.8.      In a particular design of the CMOS op amp of Fig. 10.12 the designer wishes to investigate the effects of increasing W/L ratio of both M₁ and M₂ by a factor of 4. Assuming that all other parameters are kept unchanged:

 

(a)    Find the resulting change in (|V_GS| - |V_t|) and in g_m of M₁ and M₂.

 

(b)    What change results in the voltage gain of the input stage? Also, how does this affect the overall voltage gain?

 

(c)     What is the effect on the input offset voltage?

 

(d)    If f_t is to remain the same as before the change to M₁ and M₂, what is the new value of C_C?

 

10.9.      Consider a CMOS amplifier that is complementary to that in Fig. 10.12 in which each device is replaced by its complement of the same physical size with the supplies reversed. Use the overall conditions as specified in Section 10.2.  For all devices have Spice compute I_D and the small-signal parameters g_m and r_o.  Compute the gain of the first and second stage, the overall amplifier voltage gain, the input common-mode range, and the output voltage range.

 

10.10.  Using Spice determine the frequency response behavior of the CMOS folded-cascoded op amp shown in Fig. 10.16 for a load capacitance of 1 pF, 5 pF, 10 pF, 20 pF and 100 pF. How does the amplifiers phase margin vary? 

 

10.11.  The circuit in Fig. 10.21 can be used to multiply an analog signal by a digital one by feeding the analog signal to the V_ref terminal. In this case the D/A converter is called a multiplying DAC or MDAC. Given an input sine-wave signal of 0.1sin(wt) volts, use the circuit of Fig. 10.21 together with an additional op amp to obtain v_o = 10D x sin(wt) where D is the digital word given by

 

With the aid of Spice, compute the output transient voltage waveform of the DAC for the following values of D: (i) 0110 (ii) 1111, and (iii) 0000.

 

10.12.  Repeat Problem 10.11 above, but this time, consider having the digital word D cycle through a digital pattern that resembles a symmetrical triangular waveform of 1/10-th the frequency of the input sinewave. Using the transient analysis command of Spice, plot the output voltage waveform from the MDAC.

 

10.13.  Using Spice compute the input resistance seen by V_ref in the circuit of Fig. 10.21 for all possible combinations of the switches.

 

10.14.  With the aid of Spice, compare the transfer characteristics of the D/A converter shown in Fig. 10.21 with those obtained from an identical converter experiencing a +10% increase in the value of resistor R₄.